תרשים Smith‏: ': ההיסטוריה שלו ומדוע הוא כל כך חשוב עבור מתכנני RF

מתכננים מתחילים העוסקים בתכנון RF ומנסים ליצור חיבור ישיר בין שני רכיבים - למשל, בין מתנד מבוקר מתח (VCO) לבין מערבל אותות - נתקלו ללא ספק בדפי הנתונים של רכיבים בגרפים עגולים מוזרים, כמו אלה עבור ה- MAX2472‏ מבית Maxim Integrated‏, מגבר חוצץ VCO של 500 עד 2500 מגה-הרץ (MHz) (איור 1). גרפים אלו, הנקראים תרשימי Smith, הם ללא ספק שונים מאוד מכל מה שרואים בשיעורי אלגברה או סטטיסטיקה.

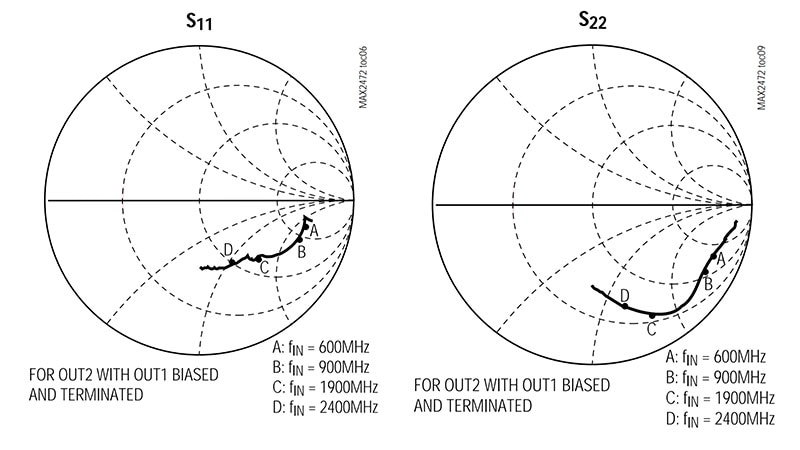איור 1: דפי נתונים רבים של רכיבי RF כוללים תרשימי Smith המציגים את הערכים של פרמטרים מרכזיים בתדרי פעולה שונים, כגון אלו עבור המגבר חוצץ MAX2472 VCO מבית Maxim‏ ב- 600, 900, 1900 ו- 2,400 מגה-הרץ (MHz‏). (מקור התמונה: Maxim Integrated)

התרשים נקרא על שמו של Phillip Smith, מהנדס בחברת Bell Telephone Laboratories, שהגה ושיכלל אותו בין 1936 ל- 1939 תוך כדי עבודה על הבנת קווי תמסורת וגלים עומדים במה שנחשב אז "תדרים גבוהים" של עד 1 מגה-הרץ (שנקראו מגה-מחזורים לשנייה באותם ימים). התרשים העגול המוזר למראה שלו הפך לכלי השימושי והחזק ביותר לעבודה ואופטימיזציה של מעגלים בתדר גבוה בהקשר של אימפדנס הכניסה והיציאה שלהם, אפילו בעידן שלנו של מחשבים רבי-עוצמה וכלי תכנון בעזרת מחשב (CAD).

בין השימושים הרבים שלו, תרשים Smith מספק דרך יעילה לדמיין אפשרויות תכנון כאשר מנסים לתאם אימפדנסים בין-דרגות של מקור ועומס, שיקול חשוב ביותר במעגלים רבים, במיוחד בתכני RF. ישנן שתי סיבות שתיאום כזה הוא קריטי:

• ראשית, כדי לממש העברת הספק מקסימלית ממקור לעומס, האימפדנס הקומפלקסי של המקור _S‏jX‏ + _S‏R‏ חייב להיות שווה לצמוד הקומפלקסי של העומס _L‏jX‏ - _L‏R‏:

כאשר R הוא החלק ההתנגדותי (האמיתי) של האימפדנס ו- X הוא החלק הראקטיבי (אינדוקטיבי או קיבולי) (איור 2).

איור 2: אתגר מרכזי בתכנון RF וקווי תמסורת הוא להבטיח שהמקור "רואה" אימפדנס עומס, שהוא הצמוד הקומפלקסי של אימפדנס המקור, גם אם אימפדנס עומס זה אינו קיים. (מקור התמונה: HandsOnRF.com)

• שנית, גם אם איבוד הספק כזה אינו מהווה שיקול (אם כי הוא כמעט תמיד), יש צורך בתיאום עכבות כדי להקטין למינימום את החזרות האנרגיה מהעומס בחזרה למקור העלולות לגרום לנזק למעגלי היציאה של המקור.

מה מראה תרשים Smith‏

תרשים Smith‏ הוא גרף קוטבי של מקדם ההחזרה הקומפלקסי (נקרא גם גמא עם הסמל (rho (Γ). הוא מציג את מה שנראה בהתחלה כמשימה כמעט בלתי אפשרית: גרף בו-זמני של החלקים האמיתיים והמדומים של אימפדנס קומפלקסי, כאשר החלק האמיתי R יכול להשתרע בין 0 לאינסוף (∞) והחלק המדומה X יכול להשתרע ממינוס אינסוף עד פלוס אינסוף - וכל זאת על גיליון נייר יחיד.

תרשים Smith‏ מפושט, המראה את מעגלי ההתנגדות הקבועה ואת קשתות האימפדנס הקבוע, הוא נקודת התחלה טובה להבנת הסידור שלו (איור 3). כיתרון נוסף, התרשים מספק גם דרך להציג את פרמטרי הפיזור (Scattering‏) (פרמטרי-S) וכיצד הערכים שלהם מתייחסים למדידות ולשיקולי החומרה בפועל.

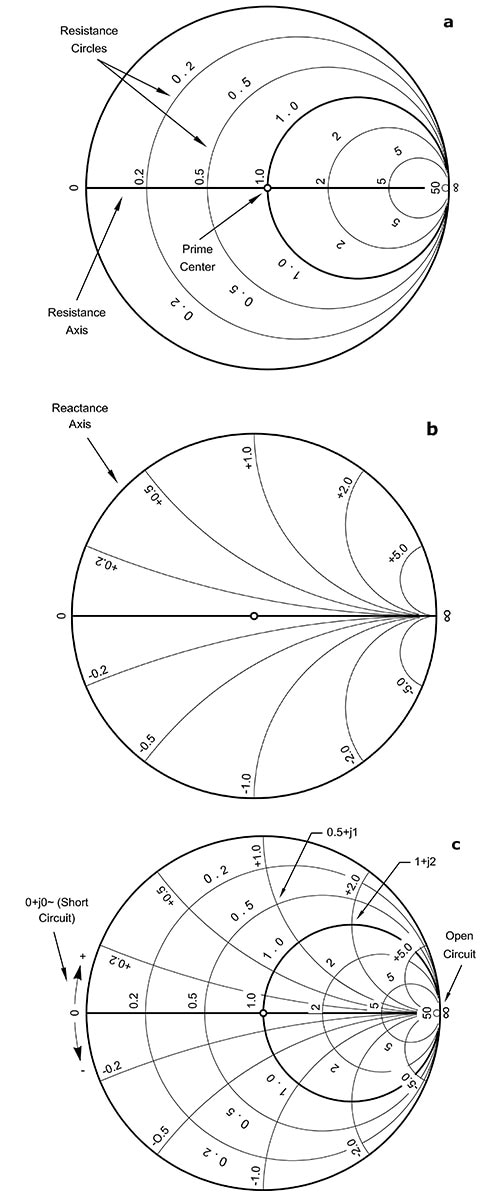איור 3: תרשים Smith מציג מעגלים של התנגדות קבועה (a) וקשתות של ראקטנס קבוע (b) המתמזגים יחד (c) כדי לתת פרספקטיבה על פני כל אפשרויות האימפדנס. (מקור התמונה: ARRL.org)

כאשר ערכי אימפדנס קומפלקסי אלו מסומנים על תרשים Smith‏, הוא יכול לשמש לזיהוי פרמטרים רבים שהם קריטיים להבנת מסלול אותות RF‏ או מצב קו התמסורת, כולל:

• מקדמי השיקוף הקומפלקסיים של המתח והזרם.
• מקדמי התמסורת הקומפלקסיים של המתח והזרם.
• מקדמי ההחזרה והתמסורת של ההספק.
• הפסדי השיקוף.
• הפסדי ההחזרה.
• גורם הפסדי גלים עומדים.
• מתח וזרם מקסימלי ומינימלי, כמו גם יחס גלים עומדים (SWR‏).
• צורה, מיקום ופילוג הפאזה ביחד עם גלים עומדים של המתח והזרם.

אבל זה רק חלק מהעוצמה של תרשים Smith‏. בעוד שהוא שימושי ולעתים קרובות הכרחי למתכננים לדעת את הפרמטרים שלעיל, תרשים Smith יכול להנחות ניתוח והחלטות תכנון כולל:

• הצגת האימפדנס הקומפלקסי לעומת התדר.
• הצגת פרמטרי S של רשת לעומת התדר.
• הערכת הראקטנס או הסוספטנס הכניסה של Stub‏ מקוצר.
• הערכת ההשפעות של אימפדנסי מצד (Shunt) או טוריים על אימפדנס קו התמסורת.
• הצגה והערכת מאפייני אימפדנס הכניסה של Stubs‏ תהודתיים ואנטי-תהודתיים, כולל רוחב-הפס וה- Q.
• תכנון רשתות תואמות-אימפדנס תוך שימוש ב- Stubs‏ פתוחים או מקוצרים יחידים או רבים, קטעי קו רבע-גל ורכיבי L-C מקובצים.

היתרונות של תרשים Smith‏

במבט ראשון, תרשים Smith‏ הסטנדרטי והמפורט במלואו עשוי להיראות כמו ערבוביה כמעט בלתי-מובנת של קווים העוברים לכל הכיוונים (איור 4), אך למעשה הוא רק עיבוד מפורט יותר ברזולוציה גבוהה יותר של התרשים הפשוט שהוצג קודם לכן. אתם יכולים להוריד גרסה להדפסה של תרשים Smith מתוך המשאבים ב- DigiKey Innovation Handbook המקוון.

איור 4: תרשים Smith‏ טיפוסי יכול להיראות מרשים, אך הוא רק עיבוד מפורט יותר ברזולוציה גבוהה יותר של התרשים הפשוט שהוצג קודם לכן. (מקור התמונה: DigiKey)

תרשים Smith מציג יותר מסתם פתרון יחיד לבעיות רבות הקשורות לתכנון: הוא מציג את הפתרונות הרבים האפשריים. לאחר מכן המתכננים יכולים להחליט אילו מהם מציעים מערכים מתאימים של ערכי רכיבים עבור המצב הספציפי, כגון ערכים מעשיים עבור משרנים וקבלים תואמי-אימפדנס. במרבית המקרים, סקאלות המספרים של התרשים "מנורמלים" למערכות 50 אוהם (Ω), מכיוון שזה האימפדנס הנפוץ ביותר בשימוש בתכני RF.

תרשים Smith הוא כל כך חשוב ושימושי עד שמכשירי בדיקה רבים עבור יישומי RF ומיקרוגל, כגון נתחי רשת וקטוריים (VNA), יכולים לשרטט ולהציג אותו. לדוגמה, ה- VNA‏ T3VNA‏ מבית Teledyne LeCroy מציע אופן כזה (איור 5).

איור 5: נתח הרשת הווקטורי T3VNA יכול להציג נתונים שנקלטו בפורמט תרשים Smith. (מקור תמונה: Teledyne LeCroy)

כמה קשה ללמוד להשתמש בתרשים Smith‏? כמו עם רוב השאלות מסוג זה, זה אותו דבר כמו לשאול תלמידים שונים איך הם מרגישים לגבי הקשיים של לימוד חשבון או תורת השדות האלקטרומגנטיים: זה תלוי. קיימים מדריכי לימוד מקוונים רבים עם טקסט וסרטונים המתחילים עם יסודות תרשים Smith ואז מוסיפים משוואות קווי תמסורת והיבטים אנליטיים. הם גם עוברים על דוגמאות רבות לשימוש בו. כמובן, ישנן גם אפליקציות ותוכנות שמקלות על ביצוע גרפים, מסגור הבעיה והערכת האפשרויות באמצעות תרשים Smith. עם זאת, זה עוזר להבין תחילה את היסודות של התרשים לפני שפונים אליהם.

סיכום

זה מדהים שכלי גרפי שפותח לפני למעלה מ- 80 שנה, הרבה לפני שתכני RF כפי שאנו מכירים אותם בכלל היו קיימים, הוא עדיין אחד המשאבים המרכזיים עבור אתגרי תכנון RF מבוססי-נייר ותוכנה כאחד. בכל אחד מהשימושים, תרשים Smith הוא כלי רב-עוצמה להצגה והערכת פרמטרי RF, והשגת תובנות לגבי חלופות התכנון והפשרות הקשורות בהן. הדרך הטובה ביותר לעמוד על עוצמתו של תרשים Smith‏ ומה הוא יכול לעשות עבורך היא להשתמש בו ולעיין בכמה מהדוגמאות הרבות שפורסמו.

קריאה מומלצת

1 - "תרשים Smith‏: כלי גרפי 'עתיק' שעדיין חיוני בתכנון RF"

https://www.digikey.com/en/articles/the-smith-chart-an-ancient-graphical-tool-still-vital-in-rf-design

2 - "מסנני SAW מצילים מוצרי אלחוט מיישומים בדידים לא-מעשיים"

https://www.digikey.com/en/articles/saw-filters-rescue-wireless-products-from-impractical-discrete-implementations

3 - "הבנת היסודות של מגברי רעש נמוך והספק בתכני אלחוט"

https://www.digikey.com/en/articles/understanding-the-basics-of-low-noise-and-power-amplifiers-in-wireless-designs

4 - "השתמשו במגברים לוגריתמיים כדי לשפר את הרגישות והביצועים בקישורי RF ואופטיים עם תחום דינמי רחב"

https://www.digikey.com/en/articles/use-log-amps-to-enhance-sensitivity-logarithmic-amplifiers